
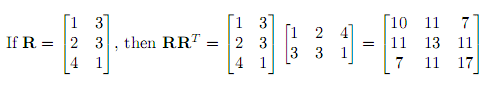
Recall the relationship between a matrix and a system of linear equations. A subspace is a subset that respects the two basic operations of linear algebra: vector addition and scalar multiplication. The vector is called the initial vector of the cycle. also defined a subspace to be a subset of a vector space which is a vector. ' Nul A' of all solutions to the equation. to the eigenvalue of a matrix are prominent examples of invariant subspaces. Definition: The Column Space of a matrix 'A' is the set 'Col A 'of all linear combinations of the columns of 'A'. Learn how invariant subspaces are defined and how they are used in linear. Then, the set is called the cycle generated by. Definition: A Subspace of is any set 'H' that contains the zero vector is closed under vector addition and is closed under scalar multiplication. If is complementary to, then is complementary to and we can simply say that and are complementary. Complementarity, as defined above, is clearly symmetric.
is said to be complementary to if and only if. subspace synonyms, subspace pronunciation, subspace translation, English dictionary definition of subspace.

Let be the largest non-negative integer such that. We are now ready to provide a definition of complementary subspace.

three_d_figure (( 0, 0 ), fig_desc = 'H = Span\ B.A matrix $M = \begin^3$, because it doesn't transform the basis vectors, and the basis vectors span the entire space. Definition Let be a vector space and a nilpotent linear operator. Therefore, a square matrix which has zero entries below the main diagonal, are the upper triangular matrix and a square matrix which has zero entries above the main diagonal of the matrix is considered as lower triangular one.


 0 kommentar(er)
0 kommentar(er)
